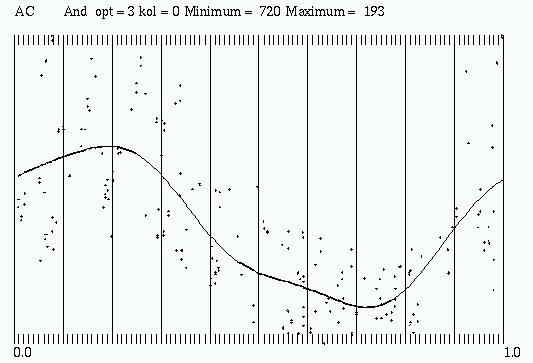
Abb. 1: Phasendarstellung der Lichtkurve von AC And aus Rotse-Daten gefaltet mit JD 2432467.373 + 0.71124243 (GCVS-Ausgangsdatum und Unterperiode p0)
Anton Paschke
Im Januar 2004 habe ich einige Arbeiten an RR-Lyrae-Sternen begonnen. Dabei bin ich bald auf AC And gestoßen, der ja alphabetisch am Anfang einer Liste erscheint.
In der Tat war er früher im BAV-RR-Lyrae-Programm 1990. Michael Dahm hat ihn bei einer Programm-Bereinigung 1999 als unvorhersagbar gestrichen, gleichzeitig mit V680 Mon, bei dem kein und KN Per, bei dem EB-Lichtwechsel festgestellt wurde (BAV Rundbrief 2/199, S. 105).
Das war mir entgangen und so habe ich an Werner Braune geschrieben mit dem Vorschlag, AC And doch zu streichen. Es gab dann noch einige Korrespondenz mit Wolfgang Renz und Werner hat uns gebeten, das Resultat doch in der Form eines Beitrages im BAV Rundbrief festzuhalten.
AC And ist früher intensiv beobachtet worden, die GEOS Datenbank enthält eine große Anzahl Maxima, die ein wirres B-R Diagramm ergeben. Im GCVS ist AC And mit einem Sternchen markiert, dazu gehört die Bemerkung, dass er keiner Klasse zuge-ordnet werden kann. Wie Wolfgang Renz aber mitgeteilt hat, wird neuerdings AC And als δ-Scuti-Stern betrachtet. δ-Scuti-Sterne pulsieren in mehreren Modi gleichzeitig. Auch unter den δ-Scuti-Sternen nimmt AC And noch eine besondere Stellung ein, weil er mit ungewöhnlich langen Perioden pulsiert.
Bei AC And werden Schwingungen mit drei Perioden beobachtet, deren Werte im GCVS und im IBVS 2046 leicht verschieden sind. Leider wird nur ein Basis-Maximum angegeben. Das wäre richtig, wenn zu dieser Zeit alle drei Schwingungen ihr Maximum hätten. Vermutlich ist es aber nur das Maximum der Schwingung mit der größten Amplitude und so fehlen uns Angaben, um auch nur eine primitive Vorhersage zu rechnen.
Ein einzelner Stern ist ja eine Kugel und wir beobachten die Schwingungen seiner Oberfläche. Jede beliebige Schwingung kann durch eine Reihe von Kugelfunktionen beschrieben werden - die Theorie stammt von Bessel und gilt als nicht ganz einfach. Ganz unverständlich ist sie aber nicht.
Nehmen wir den viel einfacheren eindimensionalen Fall, die Orgelpfeife. Das ist ein Rohr, an einem Ende offen, am anderen geschlossen. An dem geschlossenen Ende werden die Wellen gespiegelt, aus dem offenen Ende tönt es heraus. Es sind mehrere stehende Wellen möglich, bei denen die Amplitude am geschlossenen Ende gleich Null und am offenen Ende maximal ist. Je nach Länge hat die Orgelpfeife einen bestimmten Ton. Beim Grundton entspricht die Länge der Pfeife der halben Wellen-länge des Tones. Es gibt auch den Oberton, bei dem die Pfeife 1.5 Wellenlängen lang ist. Natürlich, 2.5, 3.5 und so weiter sind auch möglich. Wir haben also verschiedene Schwingungsmodi, die wir mit einem Index 0, 1, 2 usw. bezeichnen können.
Bei der Kugel ist es ähnlich. Das geschlossene Ende der Pfeife entspricht der Sternmitte, das offene Ende der Oberfläche. Auch hier haben wir verschiedene Modi, dem Grundmodus entsprechen die RRab-, dem ersten Oberton die RRc-Sterne. Dabei ist es immer noch so, dass der Stern sein ganzes Volumen aufbläht oder komprimiert. Es ist aber auch eine andere Schwingung möglich, bei der sich die Sternoberfläche am Äquator aufbläht, während die Pole einsinken und umgekehrt. Wiederum können zwischen Äquator und Pol mehr und mehr Wellen untergebracht werden. Für die müssen wir einen zweiten Index einführen. Schließlich können wird das gleiche noch in den Längengraden machen und dazu benötigen wir noch einen Index. Nun ist die Oberfläche des Sterns also schachbrettartig aufgeteilt in Regionen, die aufblähen oder absinken. Die Wellen bezeichnen wir mit einem radialen, einem Breiten- und einem Längen-Grad-Index. Solange der Stern als gasförmig betrachtet werden kann, gibt es nur die Gravitation und den Gasdruck als treibende Kräfte und in der Folge muss die Richtung der Schwingung radial sein. Wenn Astronomen von nicht radialen Schwingungen sprechen, so ist es Nachlässigkeit. Sie meinen Schwingungen, bei denen nicht nur der radiale Index größer Null ist. Erdbeben sind anders, in Festkörpern gibt es Schärwellen..
Bei der Sonne können wir die Schwingungen der Oberfläche tatsächlich beobachten, bei einem Stern beobachten wir nur die Helligkeitsänderung des gesamten Sterns als Punkt. Wir können daraus ein Schwingungs-Spektrum berechnen. Bei Orgelpfeifen rechnen wir mit Herz = Anzahl Schwingungen pro Sekunde, hier sind Schwingungen pro Tag besser geeignet.
Nehmen wir also eine bestimmte Frequenz =n 1/Periode an, falten unsere Messreihe mit dieser und legen eine Sinuskurve durch. Dabei haben wir zwei freie Parameter, die Amplitude und die Anfangsphase des Sinus. Oder praktischer: Amplituden für Sinus und Cosinus, aus denen wir dann Gesamtamplitude und Anfangsphase berechnen.
Wir berechnen den Abstand jedes Messpunktes von der Kurve, bilden das Quadrat davon und berechnen die Summe über alle Messpunkte. Die Amplitude und die Anfangsphase werden so gewählt, dass die Summe der Quadrate minimal wird. Die kleinste Summe der Quadrate entspricht der Theorie von Gaus, andere Maßzahlen für die Streuung sind auch möglich und eventuell computerfreundlicher.
Nun wird die Frequenz um einen kleinen Betrag "epsilon" verändert und die ganze Rechnung wird wiederholt. Jedes mal erhalten wir drei Werte: die Amplitude, die Phase und die residuale (verbleibende) Streuung. Tragen wir die Amplitude als Funktion der Frequenz auf, haben wir das Spektrum der Schwingungen. Alternativ können wir die Rest-Streuung auftragen, das Vorgehen bleibt im Prinzip gleich.
Zuerst suchen wir mal die höchste Linie = die wichtigste Frequenz f0. Sicher werden wir auch Linien bei der doppelten, der dreifachen usw. Frequenz finden. Das entspricht der Fourierreihe, die beispielsweise eine typische RRab-Lichtkurve beschreibt. Die Amplitude von 2*f0 ist also keineswegs durch jene von f0 bestimmt, wir müssen alle einzeln ermitteln. Wir werden auch Linien finden, die rein zufällig zustande gekommen sind. Mit Sicherheit werden wir auch eine Linie bei Frequenz 1.0 finden. Die entspricht der Erdrotation. Dazu kommen Linien bei f0+1.0, 2*f0+1.0 und so weiter.
Es gibt eine statistische Methode, mit der man abschätzen kann, ob eine Linie mit einer Amplitude A mit 99 Prozent Wahrscheinlichkeit reell (also mit 1 Prozent Wahrscheinlichkeit rein zufällig) sein könnte. Wenn wir wie oben angetönt, von der Gausschen Theorie abgewichen sind, haben wir dann Probleme. Mit zu wenigen Messpunkten werden alle gefundenen Amplituden A unter der Grenze der Glaubwürdigkeit liegen. Mit etwas Pech werden die mit der Frequenz 1.0 (Erd-rotation) verbundenen Linien das Spektrum dominieren.
Um zu entscheiden, ob eine Linie reell oder zufällig ist, braucht es vor allem mehr und genauere Messungen und diese Forderung wird nie befriedigt. Um die Frequenz von 1.0 und ihre Verwandtschaft loszuwerden, versucht man von Polargebieten oder mehreren Stationen rund um den Globus zu beobachten.
Nehmen wir also einen Stern vom Typ RRd an. Der hat noch eine Frequenz f1, in der er schwingt und wir werden auch noch Linien bei 2*f1, 3*f1, aber auch bei f0+f1, f0-f1, 2*f0+f1, 2*f0-f1 und so weiter finden. AC And haben wir damit aber noch nicht erlegt. Der hat nämlich nicht zwei, sondern drei signifikante Schwingungen. Im Spektrum werden wir also auch noch alle Linien der Art (i*f0 + j*f1 + k*f2) finden, wobei i,j,k negativ und positiv sein dürfen.
Wir haben also einen erheblichen Beobachtungs- und Rechenaufwand vor uns. Danach sind wir mit einem Wald von Spektrallinien konfrontiert, der nur mit Mühe und einem speziellen Programm zu durchschauen ist.
Das Resultat unserer Untersuchungen werden die Frequenzen f0, f1 und f2 sein, mit denen der Stern schwingt. Alle anderen Spektrallinien werden hoffentlich als eine der vielen möglichen Kombinationen erkannt. Jetzt folgt die physikalische Interpretation. Die Frequenzen f0, f1 und f2 sind am wahrscheinlichsten Grundton, erster und zweiter Oberton in radialer Richtung. So wird die Studie meistens auch veröffentlicht.
Eine Vorhersage ist damit nicht möglich. Es ist als ob man nur die Periode aber kein Basismaximum hat. In Wirklichkeit brauchen wir aber nicht nur die Amplitude und Anfangsphase für f0, f1, f2, sondern auch für alle (i*fo + j*f1 + k*f2), soweit diese als statistisch signifikant befunden wurden! Diese Zahlen werden aber nur selten veröffentlicht.
In der Rotse Datenbank sind einige Hundert Messungen von AC And und es hat mich nicht viel Arbeit gekostet, sie mit den drei bekannten Perioden p0, p1 und p2 zu falten und dabei die jeweiligen Basismaxima zu bestimmen. (Perioden nach GCVS)
51353.842 + 0.71124243 51353.585 + 0.52512637 51353.792 + 0.421069
Zum Rechnen einer Lichtkurve reicht dies nicht. Aber wenn alle drei Zyklen zusammenfallen, sollte ein schönes Maximum zu sehen sein.
Die beigegebenen, gefalteten Lichtkurven von AC And aus 216 ungefilterten CCD-Messungen des Rotse-1 Projektes (http://skydot.lanl.gov) in den Abbildungen 1 bis 3 zeigen dies aufgrund der Konstruktionsgrundlagen natürlich nicht.
Ich möchte nochmals betonen, dass eine sinnvolle Untersuchung von AC And, wie oben skizziert, wesentlich verschieden ist von dem, was BAV-Beobachter bisher mit Programmsternen taten. Es ist also richtig, den Stern aus dem BAV-Programm endgültig zu streichen. Auf der anderen Seite haben aber die Projekte Rotse und Asas einen großen Teil der bisherigen Arbeit der "Beobachtung vernachlässigter Objekte" erledigt und es ist, zumindest für die Ehrgeizigen unter uns, nötig, über die zukünftige Tätigkeit nachzudenken.

Abb. 1: Phasendarstellung der Lichtkurve von AC And aus Rotse-Daten gefaltet mit JD 2432467.373 + 0.71124243 (GCVS-Ausgangsdatum und Unterperiode p0)
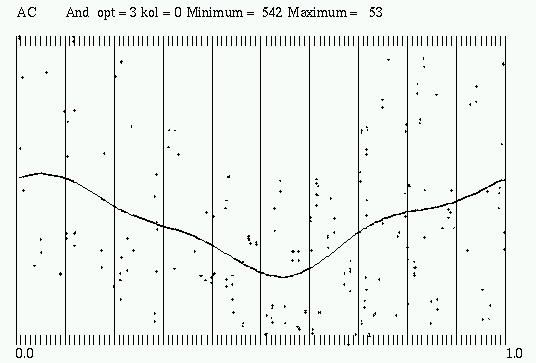
Abb. 2: Phasendarstellung der Lichtkurve von AC And aus Rotse-Daten gefaltet mit JD 2432467.373 + 0.52512637 (GCVS-Ausgangsdatum und Unterperiode p1)
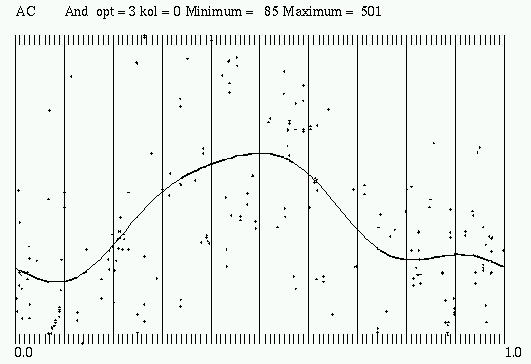
Abb. 3: Phasendarstellung der Lichtkurve von AC And aus Rotse-Daten gefaltet mit JD2432467.373 + 0.421069 (GCVS-Ausgangsdatum und Unterperiode p2)