 >
>Aqr_V0473_60990.286_G_HSR

Online-Meeting 26.01.2026 20Uhr
"Meine Beobachtungen mit dem Spektrographen
LHIRES III von Shelyak" von Jörg Schirmer (Teil 2)
Beobachtertreffen Hartha 9. Mai 2026
E0 und P werden als Elemente des Bedeckungsveränderlichen bezeichnet. Sie sind in Katalogen verzeichnet (z.B. GCVS oder J.M. Kreiner, 2004, Acta Astronomica, vol. 54).
Über längere Zeiträume hinweg, d.h. über viele Umläufe des Sternsystems betrachtet, erkennt man jedoch Abweichungen. Perioden können kürzer oder länger werden, die Exzentrizität derBahn kann sich verändern. Trägt man in einem Diagramm die Zeitdifferenz beobachtetes - rechnerisches Minimum (B-R) in ein Diagramm ein, so erkennt man häufig eine langfristige Veränderung der Umlaufzeiten der Komponenten des Systems. Das folgende Beispiel zeigt einen sinusförmigen Verlauf der (B-R)-Kurve beim Stern β Persei (Algol). Die Periode nimmt also regelmäßig zu und ab. Wir können daraus schließen, dass das Bedeckungssystem um einen dritten Stern läuft. Die Schwankung der Periode ist durch die unterschiedliche Laufzeit des Lichtes beim Umlauf um den gemeinsamen Schwerpunkt mit dem dritten Körper hervorgerufen.
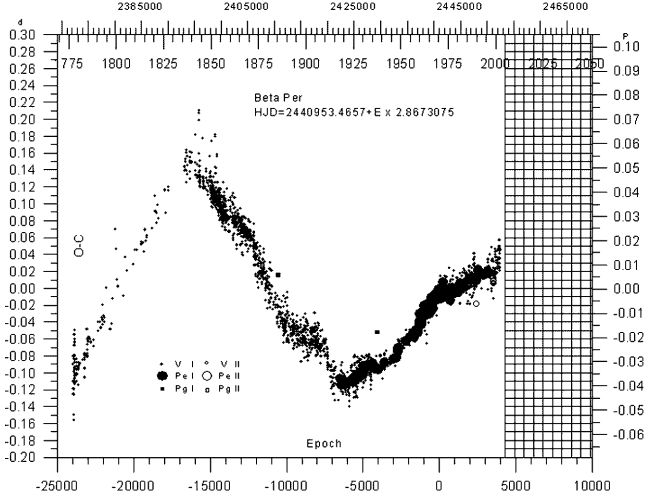
Weitere Erläuterungen zur (B-R)-Kurve siehe auch BAV Beobachtungsdatenbank und die Dokumentation zur Lichtenknecker-Database of the BAV.
Zur langfristigen Verfolgung solcher Phänomene ist die Beobachtung der Minima eines Bedeckungsveränderlichen also eine lohnende und spannende Aufgabe für den Beobachter.